Perpendicular means forming a 90-degree angle with another line, plane, or surface. In simple terms, if two things meet at a perfect right angle, they are perpendicular. This concept is fundamental in mathematics, architecture, engineering, and everyday life.
Rizz Line Generator
Understanding perpendicularity helps you recognize patterns, design structures, and solve geometry problems more efficiently. Whether you’re a student struggling with math, an engineer designing a building, or just curious about shapes around you, knowing what perpendicular means is essential.
📜 The Meaning and Definition of Perpendicular
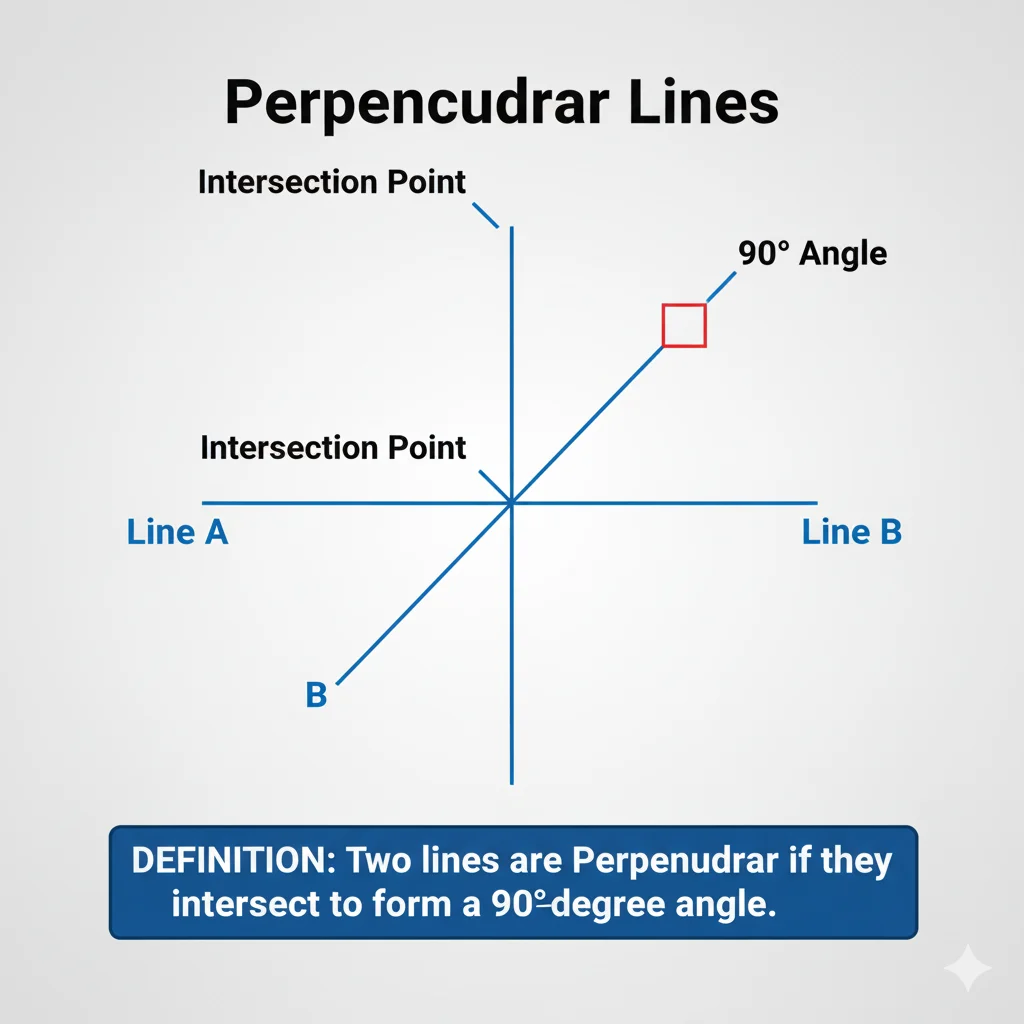
In geometry, perpendicularity is a property of two lines, a line and a plane, or two planes:
- Two lines are perpendicular if they intersect at a 90° angle.
- A line is perpendicular to a plane if it meets the plane at a right angle.
- Two planes are perpendicular if one plane contains a line that is perpendicular to the other plane.
Notation in Geometry:
If line AB is perpendicular to line CD, it is written as: AB⊥CDAB \perp CDAB⊥CD
🏗️ Perpendicular in Real Life
Perpendicularity isn’t just a math concept—it’s all around us. Recognizing it in everyday life can help you understand structures, objects, and designs:
- Buildings: Walls are perpendicular to floors.
- Furniture: Table legs are perpendicular to the tabletop.
- Roads: Streets that meet at a 90-degree intersection.
- Sports: The crossbar is perpendicular to the goalposts in soccer or football.
Fun fact: Architects and engineers rely heavily on perpendicular lines to ensure structural integrity.

🧮 Perpendicular Lines in Geometry
In geometry, perpendicular lines have some key properties:
- Intersection: Perpendicular lines always intersect.
- Right angle formation: They form a 90-degree angle.
- Slopes (in coordinate geometry):
- If a line has a slope m1m_1m1 and another line has a slope m2m_2m2, they are perpendicular if:
m1×m2=−1m_1 \times m_2 = -1m1×m2=−1
Example:
- Line 1: slope 222
- Line 2: slope −12-\frac{1}{2}−21
Since 2×−12=−12 \times -\frac{1}{2} = -12×−21=−1, the lines are perpendicular.

📊 Perpendicular vs Parallel: Comparison Table
| Feature | Perpendicular Lines | Parallel Lines |
|---|---|---|
| Intersection | Yes, at 90° | Never |
| Angle formed | 90° (Right angle) | 0° (no intersection) |
| Slopes in coordinate geometry | Product = -1 | Slopes are equal |
| Real-world examples | Walls and floors, cross streets | Railroad tracks, fence lines |
| Symbol | ⊥\perp⊥ | ∥\parallel∥ |
This table helps visual learners quickly distinguish between perpendicular and parallel lines.

🖊️ How to Draw Perpendicular Lines
Drawing perpendicular lines is simple if you follow these steps:
- Draw a line (AB).
- Use a protractor to measure 90°.
- Mark a point (C) where the perpendicular will pass.
- Draw the second line (CD) through the point at a right angle.
Tip: In coordinate geometry, you can also calculate the slope of the second line using m2=−1m1m_2 = -\frac{1}{m_1}m2=−m11.
🏫 Perpendicular in Coordinate Geometry
In the Cartesian plane:
- Equation method:
- Line 1: y=m1x+b1y = m_1x + b_1y=m1x+b1
- Line 2: y=m2x+b2y = m_2x + b_2y=m2x+b2
- Lines are perpendicular if m1⋅m2=−1m_1 \cdot m_2 = -1m1⋅m2=−1.
- Distance and intersection method:
- Perpendicular lines intersect at a 90° angle, and you can calculate distances using Pythagoras’ theorem.
Example:
- Line 1: y=3x+1y = 3x + 1y=3x+1
- Line 2: y=−13x+4y = -\frac{1}{3}x + 4y=−31x+4
- Since 3×−13=−13 \times -\frac{1}{3} = -13×−31=−1, they are perpendicular.
📐 Perpendicular in 3D Geometry
In three dimensions:
- Line to plane: A line is perpendicular to a plane if it forms a 90° angle with every line in the plane that intersects it.
- Plane to plane: Two planes are perpendicular if one contains a line perpendicular to the other plane.
Applications include:
- Engineering structures
- Construction of bridges and buildings
- Designing machinery
⚠️ Common Mistakes About Perpendicular
- Confusing perpendicular with parallel.
- Assuming lines intersect at an angle other than 90° are perpendicular.
- Not checking slope product in coordinate geometry.
- Ignoring perpendicularity in 3D geometry problems.
🎯 Tips for Understanding and Using Perpendicular
- Always look for the right angle symbol (⊥) in diagrams.
- Use a protractor to confirm perpendicularity.
- In coordinate geometry, check the slope product formula.
- Use perpendicularity in real-life constructions for better accuracy.
🏁 Conclusion
Perpendicular is more than just a geometry term—it’s a concept we see in everyday life, engineering, architecture, and sports. Recognizing perpendicular lines, planes, and surfaces helps us build stable structures, solve math problems, and understand spatial relationships.
From the classroom to real-world applications, perpendicularity is essential. Mastering this concept not only strengthens your math skills but also improves practical problem-solving and design thinking.
❓ FAQs About Perpendicular
1. What does perpendicular mean in simple words?
- It means forming a 90-degree angle with another line, plane, or surface.
2. How do you know if two lines are perpendicular?
- Check if they intersect at a right angle or if the product of their slopes = -1.
3. Can a line be perpendicular to a plane?
- Yes, if it forms a 90° angle with every line in the plane that passes through the intersection point.
4. Difference between perpendicular and parallel?
- Perpendicular lines intersect at 90°, while parallel lines never meet.
5. Where is perpendicular used in real life?
- In buildings, roads, furniture, sports fields, and engineering structures.
6. What is the symbol for perpendicular?
- The symbol is ⊥.




